NATURAL VIBRATIONS
The periodic vibrations of a body in the absence of any external force on it, are called natural (or free) vibrations.
A body clamped at one point when disturbed slightly from its rest position, starts vibrating. The vibrations so produced are called natural or free vibrations of the body. The period (or frequency) of vibration depends on the shape and size (or structure) of the body. The time period of the body is called its natural period and the frequency is called its natural frequency. A body, capable of vibrating, has a constant natural frequency of its vibrations and its amplitude of vibration remains constant. The natural vibrations of a body actually occur only in vacuum because the presence of medium around the body offers some resistance due to which the amplitude of vibration does not remain constant, but it continuously decreases.
Examples of natural (or free) vibrations
(1) If the bob of a simple pendulum is displaced slightly from its mean (or rest) position, it starts vibrating with its natural frequency which is determined by the length of the pendulum and the acceleration due to gravity g at that place. It is given as
Frequency f = 1/2π√g/l
Different pendulums (having different lengths) will vibrate with different frequencies (i.e., they will have different natural frequencies). A simple pendulum of length 1.0 m on earth's surface, where the acceleration due to gravity is 9-8 m s2, has its natural frequency 0-5 Hz.
(2) A load suspended from a spring, when stretched (or compressed) and then released, starts vibrating with its natural frequency. Its frequency is determined by the hardness (or force constant K)* of the spring and the mass 1 K m of the load (f = -). The frequency will 2n m be different for the same load on different springs and it will be different for different loads on the same spring.
(3) When a tuning fork is struck against a hard rubber pad, it vibrates with its natural frequency. The vibrations form longitudinal waves in air, which when reach our ears, sound is heard. This sound is of a single frequency (i.e., it is a pure note). Different tuning forks produce sounds of different frequencies.
(4) When an air column in a flute (or organ pipe) is made to vibrate, it vibrates with its natural frequency which is inversely proportional to the length of air column (i.e., f∞ 1/). In a flute, the notes of different frequencies are produced by changing the effective length of air column when different holes in it are closed. In an organ pipe of given length open at both ends, different modes of vibrations are produced by blowing the air differently and they are of frequencies in the ratio 1: 2: 3:...., while in an organ pipe with one end closed, the frequencies of different modes are in ratio 1:3:5:.....
Nature of natural vibrations
Natural vibrations are simple harmonic vibrations under the restoring force, the amplitude res and frequency of which remain constant. Once a body starts vibrating, it continues its vibrations we with the same amplitude and same frequency forever. Fig. 7.6 shows the displacement-time graph for natural (or free) vibrations of a body in an ideal condition.
Fig. 7.6 Displacement-time graph for natural or free vibration (in vacuum).
The vibrations of a constant amplitude can occur only in vacuum. Since in practice it is very difficult to have vacuum, it is very difficult to realise such vibrations in practice. As a matter of fact, the surrounding medium offers resistance (or friction) to the motion, so the energy of the vibrating body continuously decreases due to which the amplitude of vibration gradually decreases.
DAMPED VIBRATIONS
It is our common experience that when a body is made to vibrate in a medium, the amplitude of the vibrating body continuously decreases with time and ultimately the body stops vibrating. Such vibrations are called damped vibrations. Thus,
The periodic vibrations of a body of decreasing amplitude in presence of a resistive force are called damped vibrations.
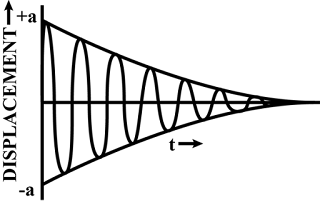
In damped vibrations, two forces act on the vibrating body: (i) the restoring force, and (ii) frictional (or resistive) force due to the surrounding medium. The amplitude of motion decreases due to the frictional force. The frictional force at any instant is proportional to the velocity of the body and it has the tendency to resist motion. As a result, the energy of the vibrating body continuously dissipates in doing work against the force of friction and so its amplitude gradually decreases. After some time, when it has lost all its energy, it stops vibrating. The energy lost by the vibrating body changes continuously into heat energy and it gets dissipated in the surrounding medium. The rate at which the energy is lost to the surroundings (or the rate of decrease of amplitude) depends on the nature (i.e., viscosity, density, etc.) of the surrounding medium and also on the shape and size of the vibrating body. Fig. 7.7 shows the displacement-time graph for a body executing damped motion.
Damped vibrations



Post a Comment